This post will be slightly different because it was written in German. German is the language of the original patents used and the main references of the literature used. Alone, to use the original terminology directly and pay homage to the inventors, I have decided to use the German language as a consistent continuation. I think that nowadays it is no longer an obstacle not to publish in English as powerful algorithms for automatic translation are available. For the captions, however, I have used English for the sake of simplicity.

Konsistente Modifikation des Kugelwellentrichters

Die Erfindung des erst später so genanten Kugelwellentrichters geht auf drei Patente der Fa. Klangfilm GmbH bzw. Siemens und Halske AG zurück und feiert bald ihren 80. Geburtstag. Eingereicht wurden 3 Patente, eines in der Schweiz (CH279947) und zwei in Deutschland (DE952179, DE955248). Alle drei Patente können über diesen Link eingesehen werden: https://worldwide.espacenet.com In den deutschen Patenten wird Friedrich Rösch als Erfinder genannt. Wie bei Patenten üblich, werden die Erfindungen bzw. die Konstruktion des Kugelwellentrichters mit viel Text beschrieben und durch einige Zeichnungen untermauert. Explizite Formeln sind dagegen Mangelware. Die ursprüngliche Bezeichnung war eher technokratisch “Lautsprechertrichter mit gekrümmtem Mantelverlauf”. Wer mehr über die Geschichte des Kugelwellentrichters erfahren möchte, den verweise ich abermals auf diese ausgezeichnete Zusammenstellung mit vielen Hintergrundinformationen (Link.1) Für meine eigenen Recherchen habe ich überwiegend auf den Artikel von H. Schmidt in der Zeitschrift “Funk und Ton”, Nr. 5, 1950, S. 226-232 (Ref.1) sowie auf das Buch von Prof. Dr.-Ing. W. Reichardt zurückgegriffen: „Grundlagen der Elektroakustik“, Akademische Verlagsgesellschaft Geest & Portig K.-G., Leipzig, 3. Auflage 1960, S. 359-362 (Ref.2), der den Artikel von H. Schmidt aufgegriffen hat und das Konstruktionsvefahren noch detaillierter beschrieben hat. Von diesem Buch konnte ich mir glücklicherweise noch ein sehr gut erhaltenes Exemplar verschaffen. Mit diesen beiden Veröffentlichungen wurde meines Wissens zum ersten Mal das Konstruktionsverfahren des Kugelwellentrichters auch mit ausreichend mathematischen Formeln und Zeichnungen beschrieben, die es dem Leser letzendlich ermöglichten, das gesamte Verfahren besser nachzuvollziehen als in den ursprunglichen Patenten dargestellt.

Der Anspruch meiner eigenen Arbeit zu dieser Thematik war nicht, lediglich die Formeln aus (Ref.1) und (Ref.2) widerzugeben sondern darüber hinaus einen neuen Meilenstein für die Beschreibung der Konstruktion aber vor allem der konsistenten Weiterentwicklung des Kugelwellentrichters zu setzen. Ich hoffe, dass ich diesem Anspruch gerecht geworden bin. Die theoretischen Grundlagen insbesondere für die Weiterentwicklung des Kugelwellentrichters können in diesem beiden Posts nachgelesen werden: Post.1, Post.2.

Zentraler Fokus dieses Posts ist vor allem, die Theorie der Konstruktion des Kugelwellentrichters noch einmal intensiv aufzuarbeiten. In meinem Spread Sheet spielt dar ideale runde Kugewellentrichter eine zentrale Rolle und bildet die Grundlage bzw. Referenz für alle angewandten Modifikationen. Daher sollen die verwendeten Formeln hier ausführlich dargestellt werden. Am Ende des Posts werden dann noch Anwendungsbeispiele auch mit Hinblick auf die bereits erwähnten Weiterentwicklungen der Streckung unter Annahme ellipsodaler Wellenfronten und der stereographischen Projektion gezeigt.

Betrachtet man zunächst den exponentiellen Schalltrichter, so ging man bei diesem zweckmäßigerweise davon aus, dass sich die Fläche der angenommenen ebenen Wellenfront A(z) exponentiell erweitert:
\tag{1} A(z) = A_{0} \cdot e^{m \cdot z}; \qquad m = \frac{4\pi \cdot f_c}{c_s}
Es war allerdings nach meinen Recherchen auch bereits eine Korrektur für gekrümmte Wellenfronten dieses Trichters bekannt, auf die hier aber nicht näher eingegangen werden soll. In Gl. (1) wird m gewöhnlich als Erweiterungsfaktor bezeichnet, f_c ist die cut-off Frequenz des Trichters und c_s die Schallgeschwindigkeit. Bei Betrachtung dieser Formel wird schnell klar, dass sich der korrespondierende Trichter unendlich erweitert. Die Erfindung des Kugelwellentrichters basierte u.a. auf experimentellen Studien, welche die Existenz einer ebenen Wellenfront in Frage stellten. Die Wellenfront musste daher insbesondere in der Nähe der Öffnung des Trichters gekrümmt sein, z.B. in Form einer Kalotte. Zudem hatte man erkannt, dass die Annahme legitim ist, dass der Radius der gekrümmten Wellenfront näherungsweise als konstant angesehen werden kann. Die konsequente Umsetzung dieser Erkenntnisse führten zum Konstruktionsverfahren der Mantellinie des neuen Trichters, wodurch eine Verbesserung gegenüber dem Exponentialtrichter erzielt werden konnte. Der Kugelwellentrichter zeigte eine deutlich breitere Abstrahlung, also weniger Bündelung und auch eine bessere Übetragung von Schallenergie unterhalb seiner unteren Grenzfrequenz. Der Abfall zu tiefen Frequenzen war zudem sehr sanft und nicht abrupt sowie nicht mit einem Peak wie beim Exponentialtrichter. Explizit wird im Patent erwähnt, dass die Austrittsöffnung des neuen Trichters senkrecht zur Trichterachse steht und auch daüber hinaus gehen kann. Das ist nach meinem Kenntnisstand auch das erste Mal, dass bei einem Trichter über eine Umrollung der Mantellinie bzw. über einen Umrollbereich explizit nachgedacht und umgesetzt wurde. Vor allem wurde auch eine deutlich kürzerer Trichter als der damalige Exponentialtrichter erreicht. Dadurch öffnet sich sich der Kugelwellentrichter natürlich deutlich schneller als der Exponentialtrichter. Die Konstruktionsvorschiften lassen sich wie folgt zusammenfassen:

• Es wird ein in der Länge konstanter Konstruktionsvektor r_k definiert, der sich aus der cut-off Frequenz des gesuchten Trichters ableiten lässt.
• Die Wellenfront ist bereits am Hals des Trichters sphärisch gekrümmt als Schnitt einer Kugeloberfläche und hat die Form einer Kalotte deren Ausgangshöhe h_0 sich rechnerisch aus dem Halsradius und dem Konstruktionsvektor ermitteln lässt. Daher ist der Startpunkt für die Berechnung der Wellenfronten im Trichterverlauf nicht am Eintritt des Trichters sondern eben bei der Höhe h_0. Es ist essentiell, diesen Aspekt verstanden zu haben.
• Die sphärische Wellenfront erweitert sich gemäß des vorgegebenen Erweiterungsfaktors, wobei sich lediglich die Höhe h der Wellenfront exponentiell vergrößert. h definiert sich als die Höhe des Kreissegments, das sich aus den Schnittpunkten des Konstruktionsvektors mit der Mantelkurve ergibt, wobei die entstehende Sekante gleichzeitig die Schnittfläche der Wellenfront aus der Kugeloberfläche mit r_k darstellt.

Aus den getroffenen Grundannnahmen ergeben sich die im Folgenden dargestellten mathematischen Beziehungen. Zunächst wird per Definition der Konstruktionsvektor r_k gemäß der gewünschten cut-off Frequenz des Trichters definiert und im Verlauf des gesamten Verfahrens konstant gehalten:
\tag{2} r_k = \frac{c_s}{\pi \cdot f_c}
Wobei c_s die Schallgeschwindigkeit darstellt und f_c die cut-off Frequenz des Trichters. f_c ist einer der beiden wesentlichen Eingabeparameter, da hierüber r_k berechnet wird. Eine mathematisch erleichterte konstruktion der Mantellinie ergibt sich unter der Annahme, dass der kostante Konstruktionsvektor den gleichen Durchmesser d_{etr} besitzt, wie ein Exponentialtrichter mit optimaler Trichteröffnung (Ref.2):
\tag{3} r_k = d_{etr} = 2 \cdot r_{etr} = \frac{4}{m}
Diese Einschränkung erschien mir aber zu extrem, die Berechnung lediglich auf diesen Spezialfall zu beschränken, da zu einer bestimmten cut-off Frequenz immer nur genau ein Halsdurchmesser passt. Aus historischen Gründen ist es aber sinnvoll, darauf hinzuweisen. Die zweite charakteristische Eigenschaft ist selbstverständlich der bereits erwähnte Halsdurchmesser d_t am Beginn des Trichters, der als Eingabeparameter definiert werden muss. Allein durch Festlegung von r_k und d_t kann der Kugelwellentrichter vollständig konstruiert werden. Das klingt einfacher als es tatsächlich der Fall ist. Der Ursprung des Konstruktionsvektors wird auf die zentrale Trichterachse gelegt und wird für die Startposition der Wellenfront derart ausgerichtet, dass seine Spitze an eine der beiden Enden des Halsdurchmessers ausgerichtet wird. Durch Rotation von r_k zum jeweils anderen Ende des Halsdurchmessers entsteht ein Kreisabschnitt mit einer Sekante. Rotiert man diese Sekante mit dem Kreisabschnitt um die Trichterachse, entsteht eine Kugelschnittfläche (Kalotte) und diese repräsentiert die bereits am Hals als gekrümmt angenommene Wellenfront. Die Höhe der Kalotte ist die gesuchte Höhe der Wellenfront am Hals h_0.

Die Höhe der Wellenfront am Hals des Trichters kann aus folgender Beziehung mit anschließender Umformung ermittelt werden:
\tag{4} r_k^2 = \left( r_k-h_0 \right)^2 + r_t^2
\tag{5} h_0 = r_k-\sqrt{r_k^2-r_t^2}
\tag{6} r_t = \frac{d_t}{2}
Die Berechnung der initialen sphärischen Wellenfront am Hals, S_0 (Mantelfläche bzw. Kalotte) kann aus den Formeln zum Kugelsegment entnommen werden (Ref.3):
\tag{7} S_{0} = 2\pi \cdot r_k \cdot h_0
Während des Konstruktionsverfahrens wandert der Konstruktionsvektor entlang der Trichterachse und bildet mit dem Radius der jeweiligen Wellenfront Sekanten sowie durch Rotation des entsprechenden Kreisabschnitts um die Trichterachse neue Wellenfronten. Dabei ist wichtig zu erwähnen, dass die angenommenen Wellenfronten nicht zwangsläufig orthogonal zur Matellinie orientiert sind, wie das z.B. bei einem Traktrix-Horn der Fall ist:

An dieser Stelle möchte ich ein Bild zeigen, was sicher in der gewählten Form etwas ungewöhnlich erscheint und auf den ersten Blick möglicherweise nicht ersichtlich wird, was es mit dem Kugelwellentrichter zu tun haben könnte. Ich finde aber, dass es sehr zum Verständnis beiträgt, wie das Konstruktionsverfahren im Detail abläuft:

Die durch r_k gebildeten Kreise veranschaulichen die Kugelwelle bzw. Segmente davon, die sich erst bei geschlossenem Profil vollständig ausbilgebildet hat und sich erst danach vom Trichterprofil ablöst und als Kugelwelle mit expandierendem Radius weiter ausbreiten kann. Es ist wichtig festzuhalten, dass sich die Kugel im gesamten Verfahren nicht ändert sondern abschnittsweise die jeweiligen Kugelsegmente als Wellenfront (Kalotte) abgetragen werden. Vielleicht wird dadurch auch klar, warum sich der Name Kugelwellentrichter etabliert hat. Die rote waagerechte Linie zeichnet die jeweilige Höhe der Wellenfont h ab. Markante Punkte sind neben dem Trichterhals und Trichtermund die maximale Ausdehung des Trichterprofils im Umrollbereich (roll-back), wo h genau gleich lang wie der Konstruktionsvektor ist und naturlich bei vollständig geschlossenem Profil, wo h zwei Mal so lang wie der Konstruktionsvektor ist. Die gestrichelte senkrechte Linie veranschaulicht die gedachte Schnittfläche für die Oberfläche der Wellenfront aus der Kugel als Kugelsegment, wobei die Schnittpunkte mit der Kugel gleichzeitig den Durchmesser der Matellinie an der Position der korrespondierenden Kalottenoberfläche abbilden. Man kann es sich so vorstellen, dass die Kugel durch die getrichelte senkrechte Linie durchgedrückt wird oder anders herum gesehen, die senkrechte getrichelte Linie durch die Kugel wandert, wobei das ausgeschnitte Segment der Kugeloberfläche zunehmend größer wird. Spezialfälle sind wieder der maxiale roll-back (genau halbe Kugeloberfläche) sowie das vollständig geschlossene Profil (ganze Kugeloberfläche). Später wird man erkennen, dass das Verfahren insbesondere im Umrollbereich nicht ganz konsistent ist, denn der Konstruktionsvektor touchiert hier etwas mit der Mantellinie, wenn sich das Profil über die maximale Ausdehnung hinaus weiter schließt. Man darf aber nicht vergessen, dass es sich lediglich um eine Konstruktionsvorschrift handelt, also die sich in der Realität ausbildenden Wellenfronten etwas anders aussehen können. Wenn sich die reale Wellenfront auch nur annähernd derart ausbreitet, wie hier dargestellt, dann habe zumindest ich großen Respekt vor dieser genialen Idee, wie der Trichter zu konstruieren ist.

Das folgende Schaubild stellt die für die weitere Betrachtung verwendeten Variablen übersichtlich dar:

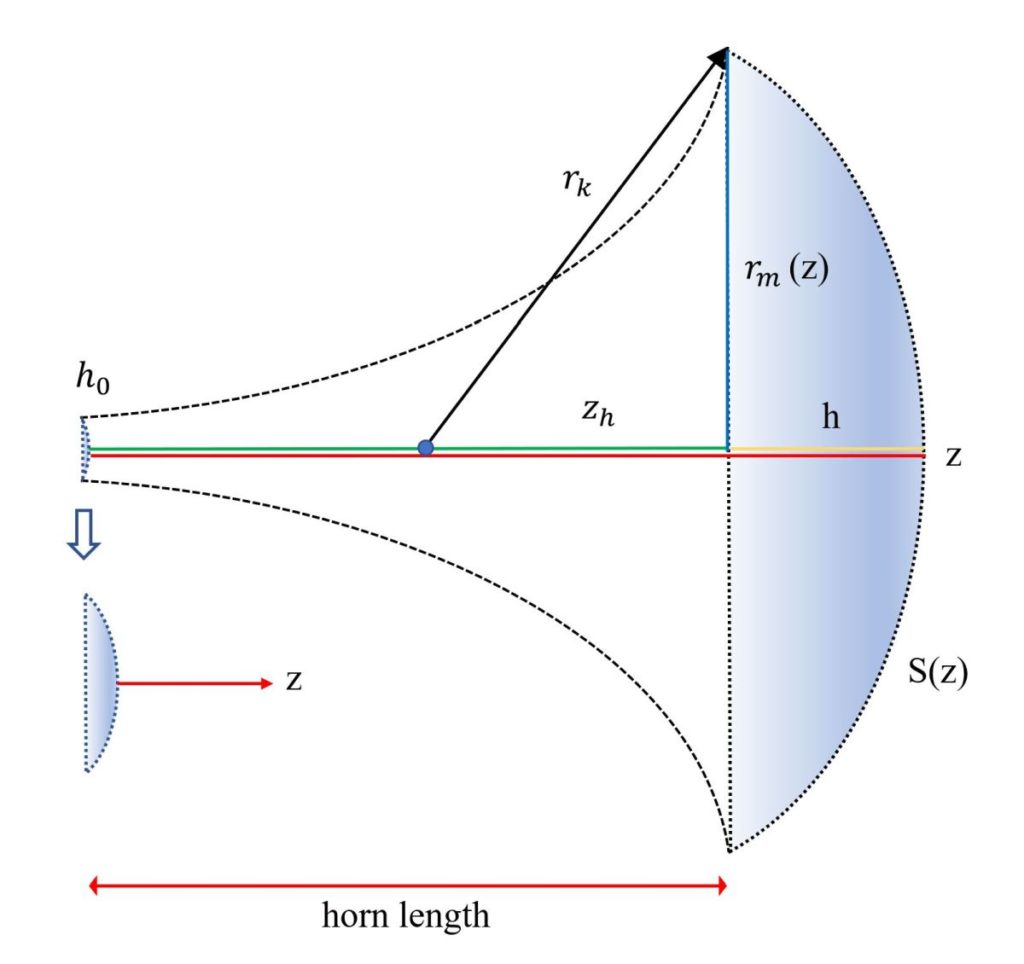
Der Unterschied bei der Konstruktion des Kugelwellentrichters zur üblichen Vorgehensweise bestand darin, dass für den Trichterverlauf nicht die Erweiterung einer ebenen Mundfläche angenommen wird sondern die Erweiterung der Fläche der gekrümmten Wellenfront gemäß des definiertem Erweiterungsfaktors. Bei konstantem r_k führt das auch zwangsläufig zu einer Umkehr der Mantellinie und zu einem geschlossenen Profil, also einem endlichen Trichter, was ein großer Vorteil war, denn üblicherweise öffnete sich die Mantellinie entweder unendlich weit wie beim Exponentialtrichter oder lief mehr oder weniger abrupt in der gedachten Montageebene des Trichtermundes aus.
Die Oberfläche der gekrümmten Wellenfront an einer beliebigen Position auf der Trichterachse z kann analog zu Gl. (7) berechnet werden.
\tag{8} S(z) = 2\pi \cdot r_k \cdot h(z)
Damit sich diese Fläche exponentiell gemäß des Erweiterungsfaktors vergrößert, muss sich bei konstantem r_k die Höhe der Wellenfront h exponentiell erweitern:
\tag{9} h(z) = h_0 \cdot e^{m \cdot z}
Mit der Oberfläche S(z) der Kalotte und der entsprechenden Höhe der Wellenfront h(z) kann nun an jeder Position z auf der Trichterachse auch der Radius der Mantellinie r_m(z) bestimmt werden:
\tag{10} r_m(z) = \sqrt{\frac{S(z)}{\pi}-h^2(z)}
Für die dazugehörige Länge auf der Trichterachse z_h vom Eintritt in den Trichter bis zum Radius der Wellenfront r_m(z) muss der Referenzpunkt der Wellenfront berücksichtigt werden:
\tag{11} z_h = z-h+h_0
Setzt man in diese Formel den Startwert z=0; \, h=h_0 ein, ergibt sich der Referenzpunkt zu:
\tag{12} z_h(0) = 0-h_0+h_0 = 0

Gewöhnlicherweise geht man zur Bestimmung der Mantellinie so vor, dass man entlang der Trichterachse Punkte mit einer definierten Schrittweite auswählt und damit die Mantellinie iterativ bestimmt und dann durch Kontrollieren der Resultate z.B. die Position des Trichtermundes abschätzt. Ist die Schrittweite ausreichend klein, mag das auch numerische relativ genau möglich sein. Zufriedenstellend ist das natürlich nicht. Man kann allerdings die charakteristischen Eigenschaften des Kugelwellentrichters wie die Trichterlänge, maximale z-Koordinate, die Höhe der Wellenfront am Trichtermund und die maximalen Ausdehnung im Umrollbereich im Voraus mathematisch exakt berechnen, ohne einen einzigen Iterationsschritt durchgeführt zu haben. Wie das geschehen kann, soll genauer untersucht werden. Die Eigenschaften der Wellenfront am Hals des Trichters wurden bereits zuvor beschrieben. Der nächste Schritt zur Ermittlung der Trichtereigenschaften sind die Verhältnisse der Parameter am Trichtermund. Die Mantellinie des Kugelwellentrichters geht genau dann in eine gedachte senkrechte Montagebene zur Trichterachse über, wenn die Änderung der Höhe der Wellenfront gleich der Änderung der z-Koordinate ist:
\tag{13} \frac{\partial h}{\partial z} = 1 = h_0 \cdot m \cdot e^{m \cdot z} = h_{mouth} \cdot m
\tag{14}h_{mouth} = \frac{1}{m}
\tag{15}z_{mouth} = \dfrac{\ln{\left(\dfrac{1}{m \cdot h_0}\right)}}{m}
\tag{16}z_{h, mouth} = z_{mouth}-h_{mouth}+h_0
Die maximale Höhe der Wellenfront ist erreicht, wenn sich das Trichterprofil schließt und die Wellenfront eine vollständige Kugeloberfläche mit dem Radius r_k bildet:
\tag{17} h_{max} = 2 \cdot r_k
Damit ist auch der größt mögliche z-Wert erreicht, weil sonst der zweite Term unter der Wurzel in Gl. (10) größer als der erste Term wird und dadurch eine negative Wurzel entstehen und das Verlassen des reellen Zahlenbereiches bedeuten würde.
\tag{18}h_{0}\cdot e^{m \cdot z_{max}} = 2 \cdot r_k
\tag{19}z_{max} = \dfrac{\ln{\left(\dfrac{2 \cdot r_k}{h_0}\right)}}{m}
\tag{20}z_{h, max} = z_{max}-2 \cdot r_k+h_0
Wir können also festhalten, dass rein mathematisch betrachtet der Kugelwellentrichter einen klar definierten Anfangspunkt und Endpunkt besitz. Es bleibt aber noch die interessante Frage, an welcher Position auf der Trichterachse die maximale Ausdehung des Trichterprofils im Umlaufbereich (roll-back) auftritt. Das ist genau dann der Fall, wenn r_k = r_m(z).
\tag{21}r_k = r_m(z) = \sqrt{\frac{S_s}{\pi}-h^2(z)}
\tag{22}r_k^2 = 2\cdot r_k \cdot h(z)-h^2(z)
\tag{23}h^2(z)-2\cdot r_k \cdot h(z)+r_k^2 = 0
Mit (23) haben wir eine allgemeine quadratische Gleichung zweiter Ordnung vorliegen und können das dafür bekannte Lösungsverfahrung, auch als pq-Formel bekannt, anwenden:
\tag{24}p = -2 \cdot r_k
\tag{25}q = r_k^2
\tag{26}h_{rb} = -p/2 \pm \sqrt{p^2/4-q}
\tag{27}z_{rb} = \dfrac{\ln{\left(\dfrac{1}{m \cdot h_{rb}}\right)}}{m}
\tag{28} z_{h, rb} = z_{rb}-h_{rb}+h_0

Ein besonders spezieller Fall beim Erreichen des Trichtermundes tritt auf, wenn der Ursprung des Konstruktionsvektors mit dem Startpunkt der Wellenfront h_{0} zusammenfällt. Dann gilt r_k = z_{mouth} und daraus resultiert genau ein passender Halsradius r_{t0}, der diese Bedingung erfüllt:
\tag{29}z_{mouth} = r_k = \dfrac{\ln{\left(\dfrac{1}{m \cdot h_0}\right)}}{m}
\tag{30} h_{t0} = \dfrac{1}{m \cdot e^{m \cdot r_k}}
\tag{31} r_{t0} = \sqrt{r_k^2-\left( r_k-h_{t0} \right)^2}
Rechnereisch vereinfachen kann man diese Ausdrücke noch, wenn man Gl. (3) berücksichtigt, in Gl. (29) einsetzt und dann umgeformt wird:
\tag{32}r_k = d_{etr} = \dfrac{d_{etr}}{4} \cdot \ln{\left(\dfrac{d_{etr}}{4} \dfrac{1}{h_{0, etr}}\right)}
\tag{33} h_{0, etr} = \dfrac{r_k}{218.3926}
\tag{34} h_{0, etr} = r_k-\sqrt{r_k^2-r_t^2}
\tag{35} r_{t, etr} = 0.0955 \cdot r_k
\tag{36} \left(\dfrac{d_{kwt}}{2}\right)^2 = r_k^2-\left(z_{mouth}-h_{mouth}\right)^2 = 2 \cdot r_k \cdot \dfrac{d_{etr}}{4} \cdot \dfrac{d_{etr}^2}{16} = \dfrac{7}{16} \cdot r_k
\tag{37}d_{kwt} = 1.3229 \cdot r_k
\tag{38}z_{h, kwt} = z_{mouth}-h_{mouth} = r_k-\frac{1}{m} = r_k-\dfrac{r_k}{4} = \frac{3}{4} \cdot r_k
Gl. (32) - (38) sind analog zu (Ref.2) formuliert und sollen eine Unterstützung bieten, falls das Interesse besteht, einen Trichter mit dieser speziellen Randbedingung zu berechnen. Dafür muss bei gegebenem Halsdurchmesser die exakt passende cut-off Fequenz herausgefunden werden, denn darüber berechnet sich wiederum r_k.

Für die iterative Berechnung des Trichterprofils als Punktwolke sollte eine sinnvolle Schrittweite der einzelnen Punkte auf der Trichterachse gefunden werden. Es wird schnell deutlich, dass man nicht einfach Punkte mit gleichem Abstand auf der Trichterachse verwenden kann, da sonst in bestimmten Bereichen, z.B. am Trichtermund sowie in der Nähe von z_{max}, das Trichterprofil nicht adäquat abgebildet wird. Die Schrittweite muss in diesen Bereichen verkürzt werden, um einen sauberen Verlauf der Mantellinie ohne sichtbare Knicke zu erhalten. Ein sinnvoller Ansatz dafür ist die Bestimmung der Bogenlänge von r_m(z):
\tag{39}l_{arc} =\int_{z_{start}}^{z_{stop}} \sqrt{1+\left(r_m^{'}(z)\right)^2} \, \partial z
\tag{40} r_m^{'}(z) = \frac{\partial r_m(z)}{\partial z}
Der mathematische Aufwand dafür ist sicher enorm, jedoch ist es für die Erstellung einer Punktwolke gerechtfertigt, da die Punkte näherungsweise gleiche Abstände voneinander haben und damit die Generierung einer sauberen Öberfläche ohne Artefakte begünstigt wird. Durch Einsetzen r_m(z) erhält man:
\tag{41} r_m(z) = \sqrt{2 \cdot r_k \cdot h_0 \cdot e^{m \cdot z}-h_0^2 \cdot e^{2 \cdot m \cdot z}}
\tag{42} r_m^{'}(z) = \dfrac{2 \cdot r_k \cdot h_0 \cdot \mathrm{e}^{m \cdot z}-2 \cdot h_0^2 \cdot m \cdot e^{2 \cdot m \cdot z}}{2\sqrt{2 \cdot r_k \cdot h_0 \cdot e^{m \cdot z}-h_0^2 \cdot e^{2 \cdot m \cdot z}}}
Für die Berechnung der Ableitung r_m^{'}(z) verwendet man besser einen der verfügbaren Online-Rechner im Netz. Das Ableiten von Formeln wie in Gl. (41) per Hand ist mühsam und fehleranfällig und schnell hat man sich dabei verzettelt. Die Bogenlänge kann nun numerisch integriert werden und zwar in der Art, dass man angefangen bei z_{start} als Anfangswert des Intervalls, z_{start} infinitesimal fortführt, bis die Bogenlänge der vorgegebenen Schrittweite entspricht und z_{stop} am Ende des Intervalls dann der neu zu berechnede Punkt auf der Trichterachse wird. Ich habe durchaus schon die Behauptung vernommen, es gäbe für die Mantellinie des Kugelwellentrichters keine direkte Formel. Dazu vertrete ich die Auffassung, dass Gleichung (41) die gesuchte Beziehung darstellt, jedoch in Abhängigkeit von der Wellenfront. Natürlich findet über die Zusatzbedingung aus Gleichung (11) sozusagen eine Transformation der Abszisse statt. Mir fehlt leider die Kenntnis über die korrekte Terminologie dieser Transformation und kann dafür auch keinen adäquaten mathematischen Begriff nennen.
Wie sieht nun so ein vollständig berechnetes Profil aus und wie steht genau der Konstruktionsvektor an bestimmten charakteristischen Punkten des Profils. Dazu habe ich folgende Zeichnung erstellt:

Und in den folgenden drei Bildern das Profil des Trichters – von links nach rechts – mit Ende am Trichtermund, maximaler Ausdehnung im Umrollbereich (roll-back) und vollständig geschlossen:

Sowie zusätzlich noch mit Umrollbereich bis maximalem roll-back bzw. vollständig geschlossen als 3D Objekte:


So schön der Umrollbereich des Trichters anzuschauen ist, darf nicht unbeachtet bleiben, dass damit die maximale Ausdehung doppelt so lang wie der Konstruktionsvektor wird. Das würde zu sehr großen Trichtern führen, lässt man die Mantellinie konsequent über den Trichtermund hinaus zurück laufen. Offenbar haben das aber schon die Erfinder seinerzeit erkannt und schlagen eine Art schnelle Rückführung der äußeren Mantellinie auf die innere Mantellinie vor. Um das zu veranschaulichen, habe ich einen Ausschnitt der entsprechenden Zeichnung aus dem originalen Patent genommen und diesen Bereich rot markiert.

Der explizite Hinweis lautete, um “Wirbelbildungen am Trichterende zu vermeiden, die bei plötzlich abgebrochenem Trichter entstehen“. Also schon damals war man sich dieses Umstandes bewusst und hat nach Lösungen für das Problem gesucht. Ich denke, wer sich gut mit CAD Programmen auskennt, der wird so einen sanften Trichterabschluss relativ einfach hinzufügen können. Ich habe mich jedoch inspirieren lassen, über mehrere mathemathische Ausdrücke die Mantellinie im Umrollbereich mit der ursprunglichen Mantellinie zu verschmelzen, um die maximale Ausdehung des Trichters in Grenzen zu halten und dennoch recht ansehnliche Formen zu generieren:
 

Nun aber zum Abschluss noch ein paar Impressionen, wie der modifizierte Kugelwellentrichter aussieht, wenn eine Transformation zu elliptischen Formen durchgeführt wird. Die Beispiele stammen von einem 400 Hz cut-off Trichter und einem Streckfaktor von 1.5, wobei verschiedenen Lamé Exponenten angewendet wurden. Zunächst eine ideale Ellipse mit Exponent 2.0:



Hier mit einem Exponent von 2.5, der von Piet Hein favorisiert wurde als ideale Superellipse:



Und als letztes Beispiel mit einem Exponenten von 6.0, wo sich die Form deutlich in Richtung rechteckig entwickelt hat:



Zum Abschluss noch eine Kombination von Stereographischer Projektion plus maximaler Rollback. Für mich sieht das resultirende Profil etwas gewöhnungsbedüftig aus, obgleich hier ein sehr sanfter Auslauf der Mantellinie ohne abrupte Abbrüche erzielt wird:


Derzeit tendiere ich aber eher dazu, dem Profil aus reiner Stereographischer Projektion den Vorzug zu geben, wobei hier sicherlich der persönliche Geschmack eine bedeutende Rolle spielt:


Durch die Stereographische Projektion wird die Mundfläche auf eine Kugeloberfläche projiziert. Die Grundidee dahinter war einerseits, Symmetrien zu brechen und damit vermeintlich Reflexionen vom Trichtermund ausgehend zurück zum Hals zu verkleinern und andererseits, die Trichterlänge vertikal zu verlängern und horizontal zu verkürzen aus den in vorhergehenden Posts genannten Gründen. In erster Linie war das mathematisch für mich eine enorme Herausforderung, die mir jedoch sehr viel Spass gemacht hat and allein das war für mich eine Bereicherung meines Hobbys. Ob die neuen Trichterprofile auch in der BEM Simulation überzeugen können, werden zukünftige Untersuchungen hoffentlich zeigen. Die ersten Ergebnisse sehen aber bereits vielversprechend aus.