It is already some years ago when I bought a pair of the 18 Sound (Eighteen Sound) large format 4 inch pure Beryllium dome compression driver ND4015Be mainly because of the recommendation from the German distributor. But to be honest I had serious concerns after my initial research in the web about the performance of this driver because of an existing review in the Voice Coil magazine:
https://audioxpress.com/article/test-bench-eighteen-sound-nd4015be-beryllium-compression-driver
I was a little bit shocked by studying the results and thought how can it be that a Beryllium driver show such a strange behaviour for the frequency response, especially the HF results confused me with a deep and quite broad notch just after 10kHz. The overall frequency response looked weird to me. In that review the ND4015Be was attached to the 18 Sound XR2064 horn which a 2 inch entry horn. If only this review had been available, the driver would never have been in my focus as I found it questionable to test this driver attached to a 2 inch entry horn. The German distributor clearly stated that there only exist one version with a 1.5 inch throat exit. But there are two adapter versions (1.5″ -> 1.4″ and 1.5″ -> 2.0″) available on request. Therefore, I strongly assume that the ND4015Be with the stock 1.5″ -> 2.0″ adapter was used to perform the tests in VC. Fortunately, I received completely different (much better) measurement figures from the distributor which convinced me to buy the drivers together with both adapter versions. Once I had the 1.5″ -> 2.0″ adapter in my hand it became quit clear to me why the test results in the Voice Coil magazine looked not as expected. This adapter is a quite short conical design with a larger exit angle and high flare rate. I have absolutely no idea why this combination was used for the tests in VC and why 18 Sound did not say anything anywhere about this review.
Anyway, I think the ND4015Be deserves a much better presentation as it performs really well. In my opinion it belongs to the best large format Beryllium compression drivers ever designed.

18 Sound ND4015Be
The overall diameter for the ND4015Be is 150mm and it’s weight 3.2kg. Below on the photo is the ND3SN which is already the larger version of the ND3 series for a comparison. Top is the Earthworks M23 microphone.
The main focus of this article is not to present absolute and calibrated numbers for a direct comparison with other published measurements but to show my distinct measurements to demonstrate the potential of this driver and to let it shine in a slightly better light in contrast to what can be found currently in the web. So be aware that the absolute dB values are almost meaningless but not the relative.
At about the same time my measurement equipment was improved, especially the measurement microphone. After some bad experiences with USB microphones I ordered an Earthworks M23 microphone and have never regretted it since then. The M23 is absolutely flat from 10Hz to 23kHz including the phase response. Earthworks provides a precise calibration file for each serial number. Only to show how good this microphone is, the correction at 10Hz is -0.01 dB and + 0.3dB at 30kHz. Besides this it has a very high sensitivity of 34mV/Pa and can drive several meters of cable without any problems. Have you ever thought about the length of your microphone cable?

Earthworks M23 Measurement Microphone
A high Bit and high sample rate audio interface is als also needed and I used a Focusrite Solo 24Bit 192kHz audio interface as signal source for all the measurements presented.
For the amplifier the choice was for the Monacor AKB-60. Is is a classic analogue small output power amplifier with low distortions and very good frequency response.
My workflow always begin with the impedance measurement of a driver without any horn as reference. CLIO Pocket was used for these tasks as it provides a one shot button feature to measure the impedance. The CLIO Pocket software has been improved and extended with more features und today I often use it for the complete workflow. This so called free-air measurement is the reference to asses how much the horn changes the impedance of the combined system driver/horn. When a driver is attached to an acoustic loading optimized horn the main resonance peak should be considerably damped and shifted to lower frequencies. We will observe this for almost all measurements as all used horns provide a fairly good loading.
For the frequency response measurements the REW software suite was used. Special emphasis was set on the relative calibration of the equipment used. The microphone M23 has it’s own calibration file provided by the manufacturer and has been stored respectively in REW. The AKB-60 was calibrated with help of REW in a pre-step and accounted for in all measurements.
As my listening room is by far no anechoic chamber I generally place the microphone near the mouth so that almost no gating is necessary and the pure driver properties become visible down to the lowest possible frequency for the driver and not the room reflections. The resulting frequency response therefore does not include the baffle loss of the horn towards lower frequencies. So far any measurements should be a reference for a cross-over design a more complicated procedure is necessary. But this procedure has been proved to simply assess the quality of each driver tested. As a rule of thumb, the curves need to be corrected down about 6dB per octave, where the horn baffle loss begins. But this topic will not be considered in more detail here, because it is of almost no importance for the qualitative assessment of the driver.
The first horn used in this series in the Stereolabs SL400Hz which is a round Tractrix horn.
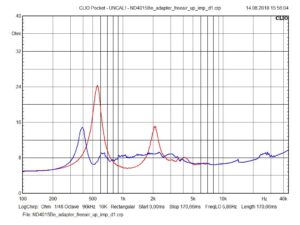
Impedance ND4015Be@SL400HZ (red=free-air; blue=attached to horn)
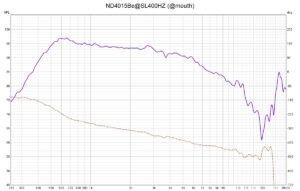
Frequency Response ND4015Be@SL400HZ
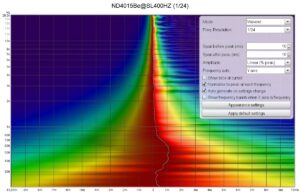
Spectrogram ND4015Be@SL400HZ
The SL400Hz with it’s Tractrix profile was never designed to provided perfect acoustic loading but it does it’s job fairly well with respect to this discipline. I don’t really like Tractrix horns because of their beaming nature and the too small mouth surface area. Just by looking at the frequency response one could already recognize the potential of the ND4015Be. The resonance frequency or break-up modes are well located beyond 20k which is typically for a Be driver. The spectrogram also show that this is a very clean driver up to 20k.
Eighteen Sound has a horn horn in the product line which fits well to the ND4015Be. The XT1464 works really good with the driver:
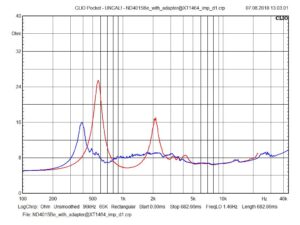
Impedance ND4015Be@XT1464 (red=free-air; blue=attached to horn)
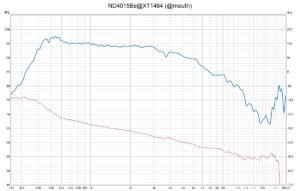
Frequency Response ND4015Be@XT1464
The main criticism I have against most modern horns like this one is that they are made out of plastic. You can feel it by touching and knocking at the surface that the material is not really high end. But this is maybe a personal preference for a solid wood constructions.
A really well and smooth performer is the Faital LTH142 horn although is is made of plastic too and I can understand why Faital uses this horn to present their 1.4 inch compression drivers:
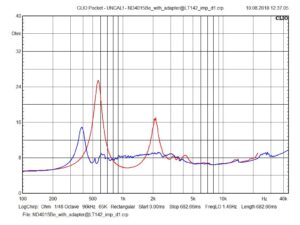
Impedance ND4015Be@LTH142 (red=free-air; blue=attached to horn)
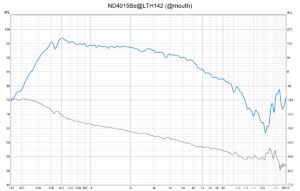
Frequency Response ND4015Be@LTH142
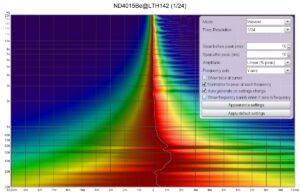
Spectrogram ND4015Be@LTH142
The frequency and phase response is close to my reference for such a large format compression driver. Just compare this curve to the Voice Coil review. It’s hard to believe that it’s the same driver model.
The next investigation was how low this driver can deliver sufficient output level. Well, the answer depends besides the driver itself on the horn attached. That time the only really low loading horn in my stock was the Selenium HL4750SLF horn. It is a quite narrow horn with a 40 x 20 radiation pattern but I used it some time for a listening session and it provided a nearly 3D soundstage representation. Honestly, the best soundstage representation so far in my setup and I believe this horn minimizes the interaction with the room because of it’s quite narrow radiation pattern. Just to emphasize that this horn does not beam within the given coverage angles. But is sounded a little bit “honky” maybe because of the almost not existing mouth flare. The HL4750SLF is a 2 inch horn so an adapter is necessary. For the tests I did not use the 18 Sound high flare adapter but ordered a longer conical metal alloy adapter.
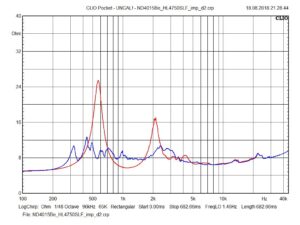
Impedance ND4015Be@HL4750SLF (red=free-air; blue=attached to horn)
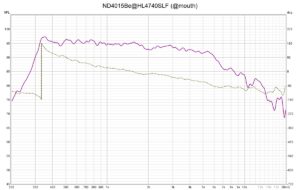
Frequency Response ND4015Be@HL4750SLF
Almost full output level down to about 300Hz and the horn seems to be the limit here. I have learned very much studying the construction plans and the manufactured pair of the HL4750SLF for my current horn developments.
My current listening setup uses the TAD TH4001 fin horn. To be able to attach the ND4015Be to this horn I designed a special adapter some years ago with the knowledge of that time. It was manufactured from solid brass with a CNC. Actually, I would make the adapter a little bit different but the older version is doing it’s job very well:
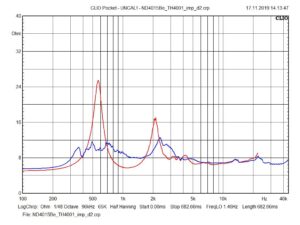
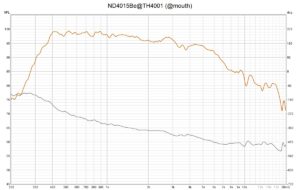
This horn is a little bit difficult to measure consistently and reproducible because of the quite large mouth surface area the fins and the measurement technique used. And although I have designed an improved fin horn, the mk3b2 radial fin horn in the meantime, I can only confirm again that listening to music with this horn is accompanied by great satisfaction. The feedback from all guests attending the TH4001 setup was consistently extremely positive.
From a private contact I got the chance to compare the Beryllium version ND4015Be to the TiN coated version NSD4015N. For this purpose I mounted both drivers to SL400HZ horn and placed the microphone a few cm in front of the mouth plane and then set the output level as high as possible. I had to leave the room during the measurements as it was seriously loud! In my opinion a very good method for distortion measurement is using REW and the RTA feature together with a stepped sine measurement:
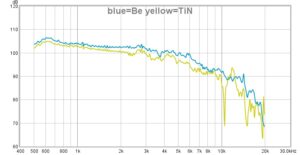
Stepped Sine Measurement: ND4015Be compared to NSD4015N
Exactly the same setup and amplifier settings were used for both drivers and then overlayed. Very good to see here that the Be driver is slightly more efficient and the HF part is much better controlled without break-up modes up to 20k. Apart from the price development of the Be version, which has become extremely expensive in the meantime I still see Beryllium for diaphragm material as benchmark for high frequency reproduction or what 18 Sound call “true piston motion”.
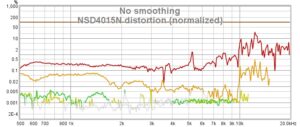
Distortion Analysis for NSD4015N
The TiN version NSD4015N is more than acceptable good up to 10k but then we face the break-up modes of the diaphragm and we see quit large distortions (2nd and 3rd harmonic).
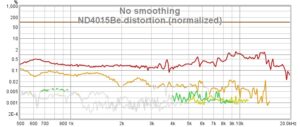
Distortion Analysis for ND4015Be
The ND4015Be remains clean at least up to 20k which is brilliant for a 4 inch diaphragm compression driver. There is a little bit raise of 2nd harmonic distortions but the 3rd harmonic remains low. The output level during these tests was extremely high and loud and would never be applied in a home setup so the real use case distortion figures should be considerably smaller.
I close this article with a clear recommendation for the ND4015Be. It is one of the very best large format compression drivers on the market. And another good thing to mention is the phase plug which ends just at the driver exit so the exit angle is almost zero or about a few degrees which leaves all possibilities to combine this driver with acoustic loading horns or faster opening wave guides.

ND4015Be Phase Plug
18 Sound has published a nice video about the ND4015 series of drivers showing also plane wave tube measurements and animations of the construction:
https://www.youtube.com/watch?v=gcPph5EuW1I









































