The next spiral function in this series is the so called Cornu spiral (Link1). Other known names are Euler or Fresnel spiral or Clotoide. The most fascinating thing is that the curvature of the Cornu spiral is proportional to it’s arc length. Therefore, it is often used as base function for car lanes or railway traces. The mathematical treatment bear some challenges as the so called Fresnel integrals have to be solved. Fortunately, these integrals can be developed as a series expansion of quite simple terms. Several examples can be found in the web an there is nothing really new about this. The biggest failure for a series expansion happens if it diverges but for the range of parameters needed for a horn it has been found that the used algorithm converges properly throughout.

In cartesian coordinates the Cornu spiral can be expressed as follows (Link2):

\tag{1a}x = a \cdot C({\phi})

\tag{1b}y = a \cdot S({\phi})

The terms C(\phi) and S(\phi) are the Fresnel integrals, a the basic length parameter and \phi the rotational angle. For the cartesian tangantial angle \psi the surprisingly easy looking expression is given as the square of the rotational angle:

\tag{2} \psi = \phi^2

Only to demonstrate that even such ugly looking integrals could sometimes be very easily programmed, I will show an example code from my first evaluation spread sheet. Later revisions got of course some more refinement:

Private Sub fresnel_cos_int(ByVal t As Double, ByRef fci As Double)
Dim sumc As Double, sumsav As Double, m1 As Double, pic As Double, piby2 As Double
Dim n As Long
pic = Application.WorksheetFunction.Pi
sumc = 0
sumsav = sumc + 0.1
n = 0
m1 = -1
piby2 = pic / 2
Do While Abs(sumc – sumsav) > 0.000002
sumsav = sumc
sumc = sumc + m1 ^ n * piby2 ^ (2 * n) / (Application.WorksheetFunction.Fact(2 * n) * (4 * n + 1)) * t ^ (4 * n + 1)
n = n + 1
If n > 50 Then
MsgBox (“!!! Error fresnel_cos_int: Series expansion is diverging !!!”)
Exit Sub
End If
Loop
fci = sumc
End Sub

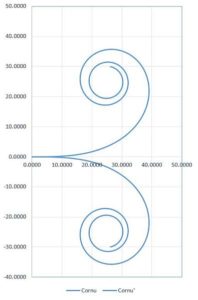
Similar to the Hyperbolic spiral it is necessary to introduce offsets for the cartesian coordinates to get the usual orientation. My first results looked like this:

         

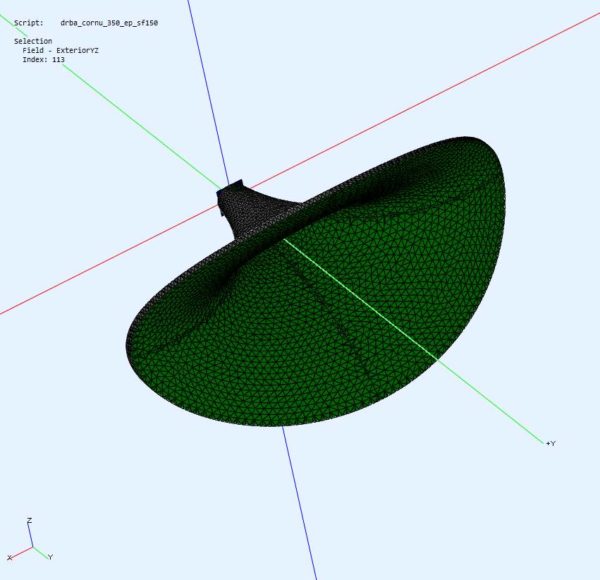
As next step the profile of the Cornu spiral was completely integrated in my DRBA calculator offering stretching options and stereographic projection. The resulting horn profile for a round 300 Hz cut-off target horn (quarter wave length optimized) can be seen in the next picture:

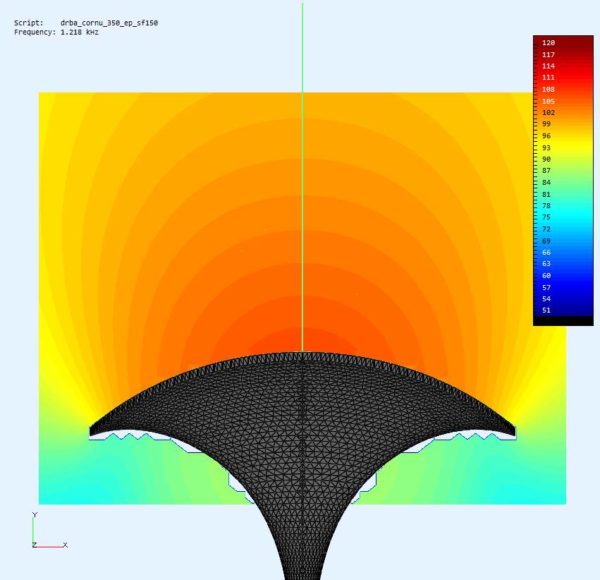
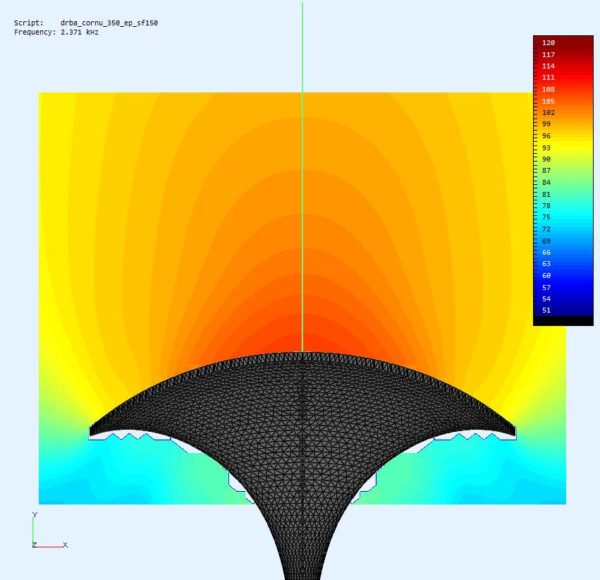
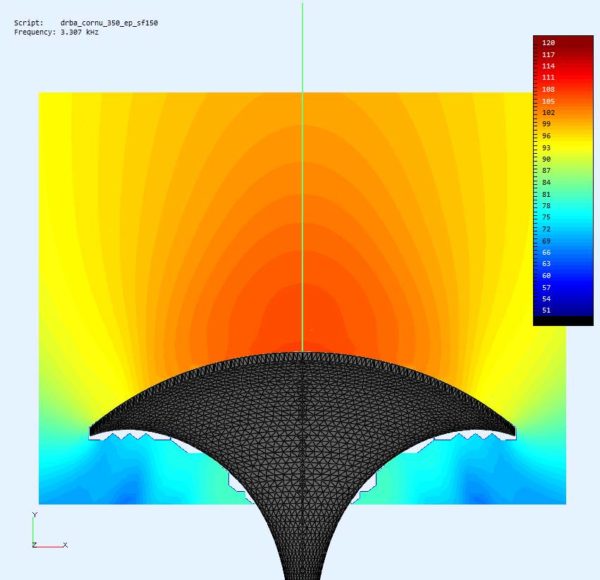
At the first view this should be quite usable for a horn profile and indeed later simulation results conform this. Some impressions of the three dimensional profile:

I will place also an STL file here for those who are interested to look at the profile with a proper CAD software:

cornu_300_rnd

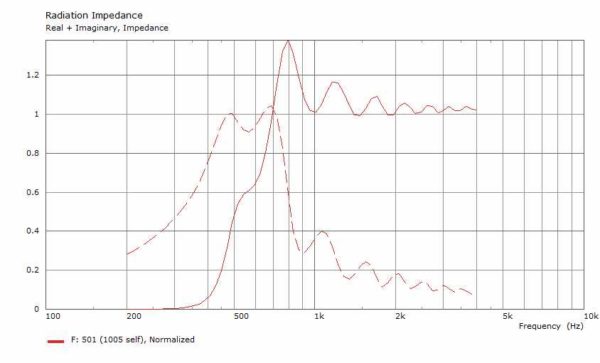
It is already some time ago when Don and me investigated this type of horn. Sadly, I can only present one simulation of of a stretched and projected profile as we focused on other topics that time. Nevertheless, the results are more than acceptable and another proof that spiral function could be a good choice for a horn profile.

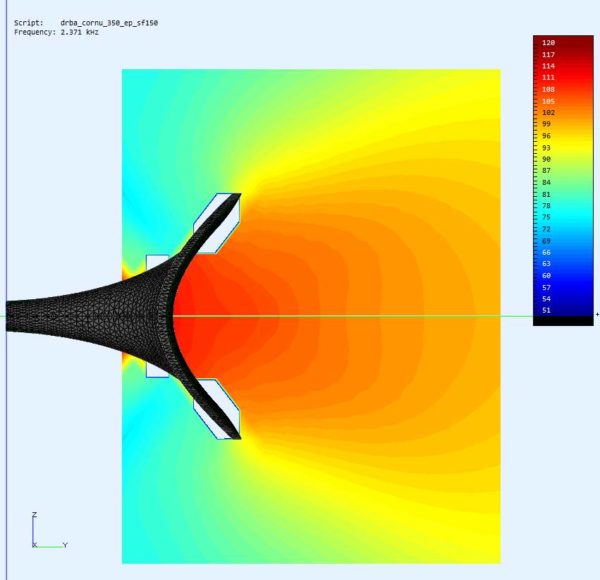
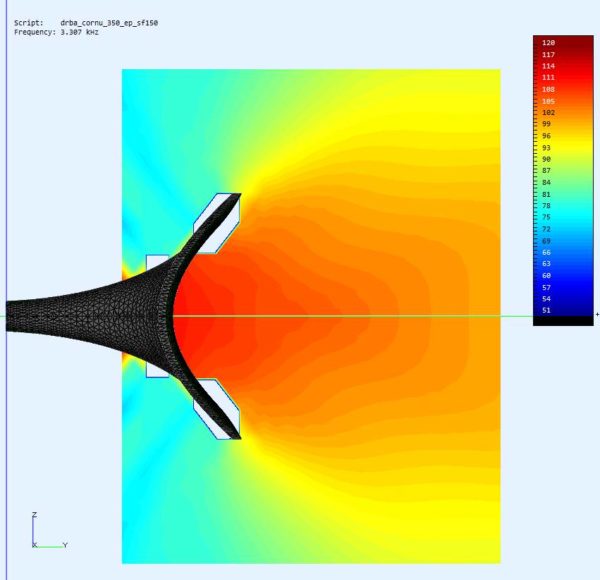
What is remarkable and I was very surprised about that, although no distinct expansion formula for a construction wave front surface area was used, the impedance curve shows a fairly straight course. A really good match as horn function if the spiral base parameters (base length and start rotational angle) have been properly defined for a given throat diameter.

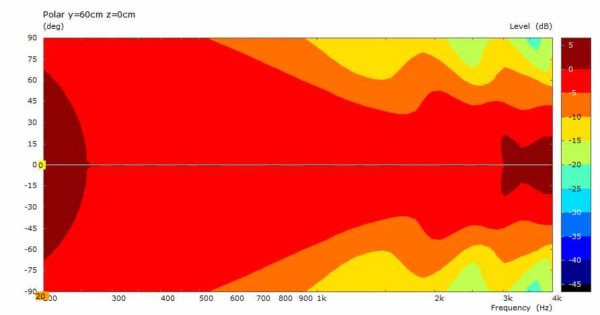
This example Cornu spiral horn was optimized for preferred horizontal dispersion. The calculation was limited up to 4k but the directivity is quite acceptable in this range. Although, I think that directivity is the most over-rated property for good horn sound. If you have ever listened to an old Western Electric snail horn like WE12a/WE13a where the sound has to travel several meters from throat to mouth then at least for me this was a day of re-thinking some HiFi terms.

And here are some examples of quite nicely looking observation fields:

It is a pleasure to see how a mathematical function, which does not necessarily come into question as a horn function at first glance, ultimately yields such good results. I am not going to publish a spread sheet for Cornu spiral now until a special interest is brought up to me.

The last function in this series, the Sici spiral, will be presented in the next post. I didn’t accidentally save this spiral function for the end of this post series, because it represents my favorite of all spiral functions presented.